I love to espouse why human factors psychology is a great path for UX research education. That said, I recognize one blind spot in my training: survey weighting. In human factors, we often rely on experimental design to mitigate concerns about individual differences and biases in our data. In UX research, we don’t often have the luxury of random assignment/experimental designs in our survey studies.

Without random assignment across groups, we enter the world of quasi-experimental design. One common quantitative UX research project like this would be tracking user attitudes over time. We can’t randomly select users for Q1 and Q2 surveys, so we can use weighting to help reduce that selection bias. We still want to isolate an effect of something on our users, but it takes a few extra steps to build evidence for any claims we have. 

Outside of quasi-experimental goals, you may just want to be sure your findings represent your entire user base as faithfully as possible. People that take surveys are unlikely to be perfectly representative in proportion to your population – survey weighting addresses this head on¹.

Weighting is a sophisticated (and complex) technique that should be employed in more surveys by UX researchers. In this post, I break down what I’ve learned and cut through some of the inconsistencies in terminology I encountered while learning about survey weighting. In part two, I’ll show a full worked example in R.

Note: this post is opinionated from my context doing in-house sampling and surveying using R. The sampling needs and procedures would differ for panel-based data, but the fundamentals I show here will still help you make sense of the right way to go about it.

Why weight surveys

Jim Lewis and Jeff Sauro recently wrote a great article about why you should (or should not) weight your survey in UX research. Weighting is framed as a method of last resort. I agree with this in the sense that you should not weight if you don’t need to. However, “last resort” makes it seem uncommon and unnecessary – this is where my experience differs working as an in-house quantitative UX researcher. They list six reasons to not use weights in your analysis (see all six reasons and notes based on my context here²), but I want to focus on two reasons they say to not weight, and why these may not apply to a typical in-house UX research context.

#1 The demographic variables that differ between the sample and the reference population don’t affect important outcome variables. 

Strictly speaking, “demographic” variables likely don’t affect important outcomes in UX research, or at least not on their surface. Things like age may be related to differing readability of font sizes, but demographics are a shorthand, in this case, for visual impairment (that is not restricted by age). 

Traditional survey weighting approaches were developed in demography and political science domains, so demographics are of key importance in that domain and the only kinds of variables with population level measures available to researchers (necessary for weighting). In most tech companies, we have access to incredibly important variables like account age, feature usage, engagement levels, etc. These kinds of variables are almost always relevant to how people respond to surveys. I’ve seen how consistently these measures influence survey results.

In tech and most modern product companies, we do have access to highly relevant user-level variables at a population scale, so we should make the most of it.

#2 The sample proportions closely match the reference population. 

Critical user variables that affect outcomes are often related to willingness or likelihood to respond to a survey. You are extremely likely to get more survey responses from engaged users and fewer responses from less engaged surveys. 

I’ve rarely seen surveys in a quantitative UX research context where the respondents simply match the population proportions.

Given these points (and the other four), I have started to weight almost all of my surveys. That said, the most common reasons I do not weight data are:

• My survey uses experimental design, like a first-click test between various prototypes.
• My survey relies on panel data so I do not have access to important population level variables (though I strongly avoid panel surveys whenever possible). 

If you are considering measuring user attitudes at scale, especially in a longitudinal tracker, I highly recommend weighting your survey results.

An overview of survey weights

We’re going to focus on the path that is most useful for UX researchers, but first let’s understand the basic landscape of survey weights. This explanation is going to be longer than my average post – even the basic landscape is complex. One distinction I don’t see mentioned often is that there are two components of any survey weights: types of weights (weighting sample/targets) and mechanism/calculation for the creation of weights.

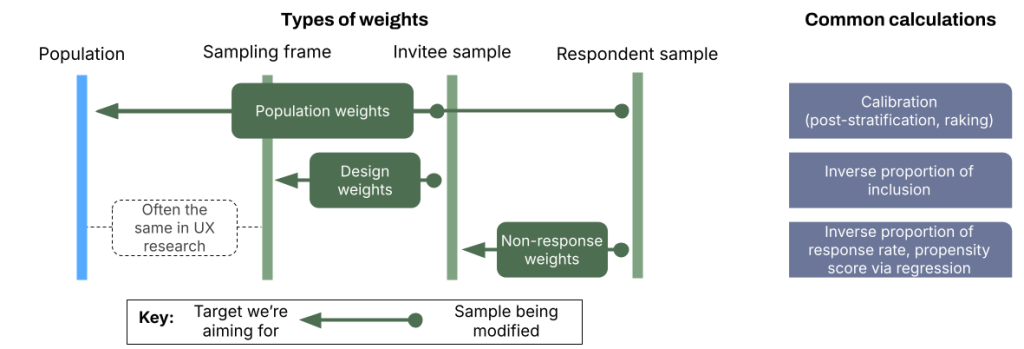
The three main types of weights are population weights, design weights, and non-response weights. Population weights in the literature are often referred to by the mechanism being used (raking/post-stratification), so it’s a non-standard term I am using. Design weights and non-response weights are calculated in a similar way and rely entirely on the sample characteristics (frame, invites, responses).

Let’s dive into each type of weight and how it’s calculated.

Notes about UX research vs. traditional survey weighting contexts:

The strongest academic tradition that developed survey weighting was political science (and demography). That context differs greatly from how we typically deploy weights in UX research, and so the existing literature can be quite confusing as a UX researcher since the available data are so different to a political scientist vs. a UX researcher.

Political science methods often rely on post-stratification weights. You have to ask about demographic variables in the survey to know who someone is. In UX research, we almost always know our variables of importance from our log data – that makes our weights stratification weights. These contextual differences are useful to consider when/if you do your own research into weighting methods. However, the math behind applying these weights is the same as each other, and both arguments in the survey package in R give the same output.

Another thing to note is the importance of a sampling frame. The sampling frame can be less reliable in political science where the sampling frame list is divorced from the need of the researcher. For example, a researcher studying learning inequities may acquire a school registration list, but this list was not gathered with that goal in mind. In UX research, the sampling frame is often fairly close to 1:1 with the population, and deviations between the two tend to be self-imposed (e.g.: don’t survey brand new users or certain high-touch segments). Further, a sampling frame for UX research gathered from a log database is often collected to better understand who users are and how to better serve them – that is fairly close to the goal of any UX research project. For in-house research purposes in UX research, we can typically consider our sampling frame to be our population for practical purposes. This allows us to fold multiple weighting steps into one without much (or any) added bias.

Design weights

Design weights account for differing chances of including a user in your invited sample compared to your sampling design. This is likely to occur when you’re intentionally oversampling users, say to achieve a big enough N in a smaller user group to compare with a bigger group.

Another common reason to create design weights are stratification weights. When you create a stratified sample, you sample from all of your sub-groups combinations separately, rather than just sending out a number of invites based on all the possible respondents in the sampling frame. The design weights in this case represent the sampling fractions from each stratum.

There are other kinds of design weights (cluster samples, multi-stage sampling, etc), but a UX researcher is unlikely to require these methods.

Calculation: 

To calculate design weights/stratification weights, we compute the inverse of the inclusion probabilities from the sampling frame/stratum to the invitee sample: 1 / (invitee sample / sample stratum).

If you have 10k users in group A and 20k in group B, and you sample 1k from group A and 1k from group B, your design weights will be 10 for group A and 20 for group B. Pragmatically, 1 response represents the responses of 10 actual users for group A and 1 response represents 20 users from group B.

Note: you can calculate your weights to give the proportion from sample invites to sampling stratum, but calculating it so each response maps to a real count of users in the population is the desired format.

Non-response weights

Non-response weights account for when fewer users in a sample, or stratified sub-sample, respond to a survey compared to the invited number. This essentially always is the case, so these are very useful (we’ll talk later about how we can calculate these within calibration weights too when our population = our sampling frame). 

Calculation: 

Design weights and non-response rates use the same formula for their calculation, but with different targets. We calculate the inverse proportion of the response rate: 1 / (respondent sample / invitee sample).

Using our design weight example, if 500 users respond from the 1k invited users of group B, then 1 response no longer accounts for 20 real users. We can calculate a non-response weight: 1 / (response N / invited N) or 1 / (500/1000) = 2.

We combine these weights by multiplying the design and non-response rates: 2 * 20 = 40. This is our final weight for group B users, so 1 response from a group B user represents 40 actual users in the population.

Another calculation method we won’t cover here is to use logistic regression to model the response propensities between the surveyed sample and the responding sample. This method is particularly useful when non-response patterns are strongly non-random or with non-probability panels (the latter is less common in our context). For the sake of simplicity, we won’t cover that method here.

Population weights

Population weights match the final respondent sample to population totals. Logistically, you’d probably pull data using SQL related to your users to get their emails or user ID’s. Counting up the full number of ID’s (often grouped by key variables), you can see your population numbers. Because you use the same data pull to choose who to invite to the survey, it’s also your sampling frame. 

There are more population weight calculation methods that could be relevant in UX research than design or non-response weights. For conciseness, I’ll focus on one method and its special cases: calibration. You can read a bit about the other options in the appendix³.

Calibration

Calibration is a method that uses inverse probabilities to make the sums of users in weighting variables match the population totals for users in those variables. The most common method of calibration is raking, likely again due to the typical data available to a political scientist where they do not have access to individual-level data for the population.

In raking, a researcher has the population margins for some variables. The procedure iteratively makes weights for each resondent until the sample weights align with the population totals. The sub-group cross tabs may not agree perfectly, but the totals will be well-matched.

By margins, I mean that you may know there are 30,000 new users/70,000 older users and 10,000 highly users/30,000 medium engaged users/80,000 low engaged users, but you don’t know how many highly engaged/new users or low engaged/older users there are. 

Example target data with marginal values used for raking:

Tenure	High	Medium	Low	Total
New user	?	?	?	30,000
Old user	?	?	?	70,000
Total	10,000	30,000	60,000	100,000

What if you do have full cross tabs of your data? 

Post-stratification weights are a specialized form of calibration weights⁴ that require a full cross tabs/contingency table (e.g.: knowing how many new/highly active users you have). It’s equivalent to setting up your raking model with one “margin”, or a single variable that is a concatenation of all your relevant weighting variables. This would mean a given set of users would have their weight calculated by the group “New User-High Engaged” and another would be “Old User-Low Engaged”, etc.

Example target data with full cross tabs for post-stratification:

Tenure	High	Medium	Low	Total
New user	3,000	9,000	18,000	30,000
Old user	7,000	21,000	42,000	70,000
Total	10,000	30,000	60,000	100,000

Note: R doesn’t use this cross tab format, it uses “long format” data, but this is better for illustration.

Because it relies on all of the sub-cells of your cross tabs, this procedure will fail if you don’t have at least one respondent that fits into each cell. This can get tricky when you have designs with many variables/levels and the resulting narrow cross tabs. Even if you do have a user in each cell, your weights may be unstable due to extremely large weights. If you don’t have respondents in each cell or you have unstable weights, it can be beneficial to use raking instead of post-stratification for more stability in your weight estimates.

Stratification weights are also mathematically similar (in many cases, identical) to post-stratification weights in their calculation. The main conceptual difference is that you create your stratification weights as you create the sample (like we talked about regarding design weights), so you create the weights before you even send the survey. This difference matters more in contexts where you don’t have reliable access to individual level data for weighting variables⁵. 

Let me summarize this section on calibration. Calibration colloquially refers to raking, where you iteratively adjust weights to match population margins. Post-stratification is technically just calibration where you use full cross tabs of weight variables rather than marginal totals for each variable. Stratification design weights are often calculated in the same way as post-stratification population weights when your sampling frame is identical to your population. 

Putting weights into practice

What to variables to choose

Variable selection is a critical process in weighting your survey. If you’ve already run surveys, look at the historical data to see what kinds of users show a high or low non-response rate. Commonly, less engaged users take fewer surveys. You can imagine that, despite this, you want to represent their viewpoint well because product teams probably want to know why they are not engaged with the product.

Outside of non-response, see if certain user groups tend to respond differently to Likert scale or attitudinal questions. I avoid demographic variables in UX research, but country is one that I do end up using. Country is a major source of measurement bias in survey responses and often important to the business for growth strategy. Other classic things to consider are skill/experience level (for which tenure on the platform could be a proxy) or key feature usage.

Once you have a set of weighting variables identified, you may find that they apply well to any survey study using that population.

What tools to use

I am an avid R user, so I use R for survey weighting. SAS and Stata are also useful tools for survey weighting (but cost money/aren’t widely used in tech).

You can technically do a manual form of post-stratification in Excel/Google Sheets, but it’s a bit clunky. If you need to hack it with Excel/Sheets, MeasuringU wrote another article that will tell you how. While they don’t name it as such, they give a method for 1-step post-stratification (as I’ll give an overview of below in R).

Survey weighting is advanced enough that it requires more specialized tools. Even python doesn’t have the same robustness of packages that R has in this domain.

I believe that R is the best option with the foundational package survey doing the heavy lifting and srvyr helping clean up the code in a tidy format. I also really like the autumn package for quick raking in a tidy format (though it’s not yet on CRAN).

The most common way I weight a survey

Technically, when you have the data available, you can or should do a 3 step process of calculating design weights, non-response weights, and then population weights. Most of the time in UX research, you can do a highly effective job with only population weights. This is especially true when your population and sampling frame are the same, so it’s the path I take most often.

Using the post-stratification procedure in the R package survey, you can account for the design/population weights (when population = sampling frame) and the survey non-response rates in a single step. Creating all of the weights separately will more effectively account for unique biases at each step, but a 1-step weighting procedure will normally suffice⁶. 

Here are the major steps in how I weight survey data:

1. Pull population level data in SQL that includes key weighting variables
2. Use GROUP BY to count the sub-group (strata) totals for my key weighting variables
3. Sample the desired N of users to invite to the survey
4. Invite users and launch the survey
5. In R, bring in the survey response data that contains key weighting variables attached for each respondent
6. Bring in the aggregated data to R from step #2 to have population level data for post-stratification
7. Use the survey package to calculate weights (technically using the post-stratification method for population weights, but realistically covering design and non-response weights in 1 step)
8. Use the survey and srvyr package to model the data.
   1. Model is a fancy word: it can mean regressions but it can also just be averages and confidence intervals. 
   2. Note: not all functions in R that can use a “weight” argument for survey weights. For example, the base glm() function has a weight argument that does not work for survey weights.

Using post-stratification is not the most technically correct method, but it gets identical results for typical situations in UX research surveys of low to moderate complexity. When my cross tabs get very small (like when weighting across a few variables and 10+ countries), I may turn to raking to provide more stable estimates. To do this I’ll modify step #2 to calculate population margins from the same data and modify step #7 to calculate rake weights (in the same package or with the autumn package). 

Wrapping up

Survey weighting is a useful tool to reduce bias in your survey samples and better understand what results are truly due to product changes. It can be a complex and tedious method, depending on how you sample and design your survey. In-house UX researchers are in a luxurious position to have individual-level, population-wide data. This context allows us to use relatively simple procedures to effectively calculate our survey weights.

In part two, I’ll cover a fully reproducible example in R for weighting survey data.

Thanks to Daniel Guzman for a conversation that helped to clarify my thinking, in particular about trade offs for computing multiple weight types in a single step.
Thanks for Ben Morse for his notes about logistic regression propensity scores for non-response modeling.

Appendix

1. A colleague of mine at Meta once said that “people who take surveys are fucking weird”. I agree with that statement (and I am also someone that takes surveys). Nate Silver has also said “People who answer polls are kind of freaks”. I like to think of these statements as more playful than anything, but important to consider how aggressively and often we should be dealing with response biases in surveys. Even in qualitative work, it’s easy to imagine that the average person to agree to a usability test differs in some way from the rest of the population (in the Big 5, we may say openness to experience). ↩︎
2. In an in-house quantitative UX research context, many of the reasons cited to not weight do not apply on a typical project. 
   
   There is no need to match a reference population. 
   We do want to estimate our findings to our population, especially in quant UX research. While this may not apply as often to things like classic usability problem discovery (you don’t need to trip on a rug twice to fix it), it does apply when a part of the quantitative UX researcher’s remit is scaling insights to the entire user base. 
   The demographic variables that differ between the sample and the reference population don’t affect important outcome variables. 
   In my personal experience, there are often deep grooves in our user populations. They are rarely demographic, but often measurable (like engagement levels). These variables are highly likely to affect important outcomes.
   The sample proportions closely match the reference population. 
   Again, in my personal experience, response proportions often vary greatly based on things like engagement levels or experience levels. I’d be surprised if my sample simply matched my population proportion.
   It’s more important for estimates to be precise than match a reference population. 
   This is certainly true, but it becomes philosophical – when is precision more important if it measures the underlying population inaccurately?
   There is no reliable reference population.
   This is often not the case in tech companies or even non-tech companies that have data-empowered users. It could be more difficult in high security environments like healthcare, but many places make it feasible to get population level data.
   Sample sizes are very small for key groups. 
   This holds, but is more a threat to survey methodologies in general for a quant UX researcher. One thing to note about survey weighting is that your power calculations will become more complicated and the necessary sample size will increase. ↩︎
3. Pew Research Center has a great article explaining common population weighting methods. I talk about calibration above, and here are the other two they cover:
   
   Matching 
   Matching involves the selection of an “ideal” sample representing the true population. Machine learning techniques are then employed to see if each additional response matches a case in the ideal sample. If not, the cases are discarded. This sample results in a loss of data and depends on building an ideal sample. This is quite complex and results in a loss of data, so I use calibration in my surveys.
   
   Propensity weighting
   Propensity weighting is conceptually similar to how design weights are calculated: you weight each case by the inverse of its probability of response. Unlike design weights, this typically uses machine learning models, like random forests, or simply logistic regression to estimate the probability of a response. Like matching, I avoid this method because it’s more complex and it can lead to larger margins of error. 
   The pew article describes that using this in addition to raking is more effective than raking alone, but we’re striking a balance of complexity and usability. Ultimately, your variable selection is more important than weight calculation procedures and we don’t need to use ML to make effective survey weights most of the time.
   ↩︎
4. This article was truly enlightening – I would encourage everyone who reads and values my post to also read this full text. It’s informative and easy to follow.
   
   “In view of calibration/raking, post-stratification is simply calibration with one margin (although it may be a complicated margin with two- or three-way interactions). I implement the true post-stratification simply by running my Stata program with one single target.” ↩︎
5. When we have variables we want to weight by in UX research (especially with in-house product teams), the variables we have of interest are from log data. This means we can get the population level counts, but we can also attach those to each individual user we sample and that responds. This technically means we can stratify our data, rather than just post-stratify, even if we change our sampling plan after we launch the survey (since we have all the individual level data).. For moderately simple surveys, both paths will result in the exact same estimates and variances, so don’t worry too much about this. ↩︎
6. I ran a quick test with a basic simulated data set and one weighting variable with two categories. This won’t extend to complex survey designs, but you can see how similar the weights are across 1 and 2 step weighting procedures with stratification and post-stratification. You’ll see some of these data again in Part II.
   
   
   ↩︎
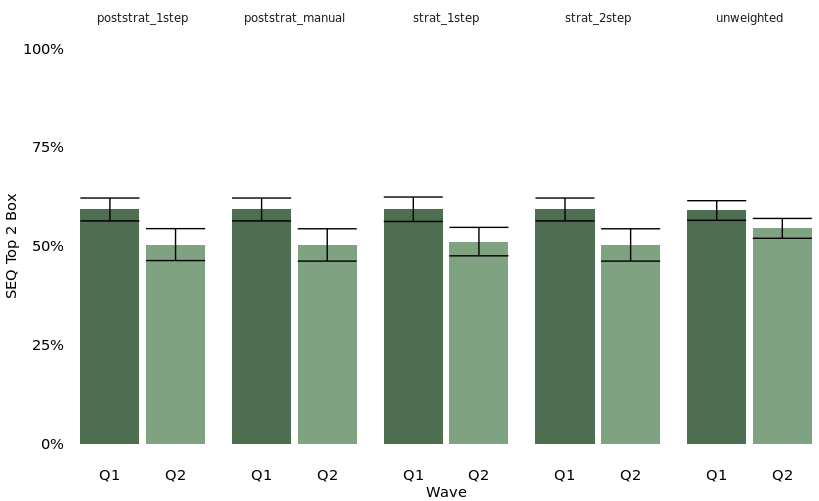